ディペンデンシー グラフ(DG)は、コネクトされた構成要素の集合です。DAG とは異なり、このコネクションは循環可能で、親子リレーションシップを持ちません。その代わりにグラフのコネクションによって、グラフのある構成要素から別の構成要素にデータを移動できます。グラフ内でデータの受け取りと出力を行う構成要素は、ディペンデンシー グラフ ノードと呼ばれます。
ディペンデンシー グラフ ノードは、計算を行うディペンデンシー グラフの一部です。ノードは入力データのセット(別のノードへのコネクションによって提供されるか、単純に与えられます)を取り、これを使用して出力データのセットを作成します。ディペンデンシー グラフ ノードは、モデル作成、デフォメーション、アニメーション、オーディオ処理など、Maya のほとんどすべてで使用されます。
Maya のほとんどのオブジェクトは、ディペンデンシー グラフ ノードか、ノードのネットワーク(複数のノードがコネクトされたもの)です。たとえば DAG ノードはディペンデンシー グラフ ノードで、シェーダはノードのネットワークです。
ディペンデンシー グラフ ノード同士がコネクトされると、DAG ノードが影響され、レンダーされるものも影響を受けます。
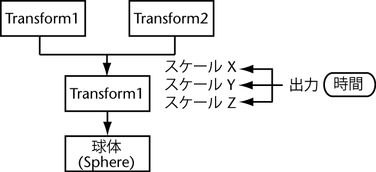
この図では、DAG 階層とディペンデンシー グラフを結合しています。Transform1、Transform2、Transform3、および球体(Sphere)がすべて DAG ノードである一方(ディペンデンシー グラフ ノードでもあります)、時間(Time)は単なるディペンデンシー グラフ ノードです。
Transform3 のスケール X(Scale X)、スケール Y(Scale Y)、スケール Z(Scale Z)パラメータは時間の影響を受けています。あるいは、時間の出力が、Transform3 のスケール X、スケール Y、スケール Z のコネクションに接続されていると考えることもできます。アニメーションの再生時には、球体の 2 つのインスタンスのサイズが大きくなります。
グラフ内を流れるデータは、数値のように単純な場合もあれば、サーフェスのように複雑な場合もあります。完全なユーザ定義オブジェクトである場合もあります。
ディペンデンシー グラフは非常に複雑なアーキテクチャで構成されており、その動作を完全に説明すると、もう 1 冊マニュアルが書けてしまいます。ここでは、簡潔に説明します。
前に説明したように、ディペンデンシー グラフは有向グラフで、グラフのエッジは別のノードのプラグをコネクトします。データはこのエッジに沿って送信されます。データには、数値、ベクトル、行列などの基本の型、およびカーブ、サーフェス、ユーザ定義型などの複雑な型が含まれます。
Maya ノードの定義の一部として、どの入力アトリビュートがどの出力アトリビュートに影響するかを指定する必要があります(API では、MPxNode::attributeAffects メソッドで実行します)。
ノードのアトリビュートが変更されると、ディペンデンシー グラフは、そのアトリビュートが出力に影響するかどうかチェックします。影響する場合は、それぞれの出力がダーティ(dirty)とマークされます。これは、キャッシュされている値が古く、再計算の必要があるということを表します。出力アトリビュートごとに、ディペンデンシー グラフは、それがコネクションのソースになっているかどうか確認します。ソースになっている場合はコネクションがたどられ、たどられたアトリビュートもダーティとマークされます。この処理が繰り返され、最終的には、グラフ内の計算し直す必要があるノードのすべてのアトリビュートがダーティとマークされます。この時点では、どのアトリビュートも再計算されないことに注意してください。その代わりに状態が更新され、どのデータが無効であるかを認識できるようになります。無効なアトリビュートの評価と再計算は、別々のステップで実行されます。
画面のリフレッシュやアニメーションの再生など、特定のイベントによって、ディペンデンシー グラフの再評価が引き起こされることがあります。たとえばリフレッシュ中は、システムが DAG を走査し、DAG ノードごとに再評価の必要があるかどうかを確認します(プラグがダーティであるかどうかチェックします)。再評価の必要がある場合は、プラグに影響するノードの compute メソッドがコールされます。この compute メソッドは、ダーティなプラグに依存している可能性があるので、影響するノードの compute メソッドもコールされます。このようにして、DG の関連する部分で、再評価が必要な部分のみが再評価されます。
最適化のために、DG は必要にならないとグラフを再評価しません。たとえば、3 つのノードがある回転サーフェスを考えます。あるカーブ DAG ノードが、カーブを回転してサーフェスを作成する第 2 ノードの入力として使用され、それが第 3 ノード、すなわちサーフェスを DAG に配置する DAG ノードの出力となっている関係です。入力カーブを修正しても、サーフェスはすぐには再作成されません。再作成は画面が次にリフレッシュされるまで行われません。最終的にサーフェスが確実に再作成されるようにするため、カーブを修正すると、カーブの出力プラグにコネクトされているすべてのプラグがダーティとマークされ、回転ノードの入力もダーティとマークされます(カーブの出力プラグ自体は、再計算されたばかりなのでダーティとマークされません)。アトリビュートを宣言する場合には、相互に影響するアトリビュートを指定する必要があります。回転ノードでは、出力アトリビュートは入力アトリビュートに依存します。このため入力アトリビュートをダーティとマークすると、出力アトリビュートもダーティとマークされます。回転ノードの出力はサーフェス ノードにコネクトされているので、回転ノードの出力がダーティとマークされると、サーフェスもダーティとマークされます。このため、画面のリフレッシュ中に DAG が走査されると、サーフェスがダーティとマークされているので、ダーティとマークされているものに依存するすべてが再評価される必要があります。
再評価は、ダーティとマークされた入力を含まない最初のノードで停止します。たとえばカーブの回転角度を変更したが、カーブ自体は変更しなかった場合、回転サーフェスの再作成により、回転ノードは再計算されますが、カーブは影響されません。
これは高レベルでの説明です。実際はいろいろ複雑な判断が行われ、必要ない評価は実行されません。
グラフ内を流れるデータは、パイプ内を流れる水にたとえられます。パイプ自体は接続(コネクション)にあたり、流れるデータがなければパイプは何も行いません。
このたとえを拡張すると、ノードは、栓、シャワー、噴水、トイレ、泉、自動歯ブラシにたとえられます。それぞれ独自の方法で水を使用して何らかを行いますが、水がないと動作しません。
DG を使用する場合の興味深い副作用は、オブジェクトに直接影響を与えるのが難しくなることです。
たとえば、前の図の球体を考えてください。Transform3 のスケールに DG ノードがコネクトされていなければ、UI か API で設定した値が新しいスケールになります。しかし図のように 時間が球体のスケールに影響する場合、Transform3 のスケールを UI か API でさらに修正しても、結果は異なったものになります。スケールを設定すると、ディペンデンシー グラフが次に再評価されるまで、時間によって設定された値をオーバーライドしますが、再評価と同時に UI または API で設定した値は、時間により再度オーバーライドされます。
回転サーフェスはより複雑な例です。作成されたサーフェス上の CV を移動したら、何が起きるでしょうか。CV は、DG が再評価されるまで新しい位置に移動しますが、再評価された時点で、回転ノードが指示する位置に戻ります。
しかしモデルの微調整は、複雑なモデルやシーンの作成に必要な操作です。そこで Maya では、この調整を処理するメカニズムを設計しました。メッシュ シェイプはアトリビュート pnts を持ちます。ここには、メッシュの頂点に加えたローカルな変更が保存されます。メッシュの頂点の新しいセットを生成するメッシュ シェイプ ノードの上流コネクションは、pnts アトリビュートに影響しません。pnts アトリビュートの値は、メッシュの座標に追加されます。NURBS サーフェス、および制御点に基づくその他のノードでは、controlPoints アトリビュートに調整情報が保存されます。Maya では、制御点に基づくノードの調整情報を保存する ツィーク(Tweak)ノードも実装されています。ツィーク ノードは、制御点に基づくノード、および制御点上で動作する上流トランスフォーム ノードの間に配置されます。ツィーク ノードは、調整情報と変形制御点を統合し、最終的な制御点を生成してシェイプに渡します。調整情報を処理するアトリビュートの詳細については、「ツィーク ノード」、「メッシュシェイプ ノード」、「NURBS サーフェスシェイプ ノード」のマニュアル ページを参照してください。